
Deux problèmes de minimum
D'après un énoncé trouvé
sur www.ac-lille.fr
Premier problème : la forme des alvéoles - Recherche de polygones réguliers qui permettent de réaliser un pavage du plan
1. Soit n un nombre entier naturel
supérieur ou égal à 3. Soit A1A2…An
un polygone régulier à n côtés. Soit O le centre
du cercle circonscrit au polygone. Les n côtés ont la même
longueur et les angles A1A2A3, A2A3A4,…
ont la même mesure. On divise le polygone en n triangles AiOAi+1,
tous isocèles en O, dont les côtés opposés
à O sont les côtés du polygone. |
 |
Montrer que la mesure en radians de chaque angle AiAi+1Ai+2
est égale à ![]()
La somme des angles a
est égale à 2p
, donc la valeur d’un angle a
est égale à ![]() .
.
De ce fait,  car
car ![]() (somme des angles d’un triangle)
(somme des angles d’un triangle)
Et l’angle![]() , CQFD
, CQFD
Montrer que la réalisation d’un pavage du plan avec des polygones
réguliers à n côtés, n ≥ 3 n’est possible que si ![]() est un nombre entier naturel.
est un nombre entier naturel.
On a vu que les angles des polygones étaient égaux à ![]() .
.
Quand on accole k polygones, la somme des angles AiAi+1Ai+2 est égale à 2π, d’où

Il faut que k (k étant le nombre de polygones que l’on accole) soit entier pour que la réalisation du pavage du plan puisse se faire sans qu’il reste d’espace libre ou que les polygones se chevauchent.
On considère la suite définie pour tout entier
naturel n supérieur ou égal à trois par ![]()
Sens de variation de la suite Un :
On pose![]()
Or

Donc plus le nombre de côtés des polygones est élevé, moins on peut en accoler.
Limite de Un :
![]() (limite à l’infini d’une fonction rationnelle)
(limite à l’infini d’une fonction rationnelle)
__________________________________________
![]()
![]()
![]()
![]() => pas entier
=> pas entier
![]()
![]() Or
Or ![]() .
.
On cherche un nombre k entier et strictement supérieur à 2. Comme Un est décroissante et tend vers 2, la démonstration s’arrête ici car on ne trouvera plus aucun Un entier et strictement supérieur à 2.
On peut donc en déduire que les seules valeurs de n pour lesquelles k est un entier sont 3, 4 et 6. On ne peut donc réaliser un pavage du plan avec des polygones réguliers que si ces polygones sont des triangles, des carrés ou des hexagones.
2.A On suppose que le périmètre du polygone est constant et égal à P
Soit n un nombre entier naturel supérieur ou égal à 3, I l’intervalle [3 ; +∞[On suppose que le périmètre du polygone est constant et égal à p.
On note Sn l’aire d’un polygone régulier à n côtés de périmètre p.
Sn en fonction de p
 |
On divise le polygone en n triangles
isocèles, comme au début. |


Or l’aire S du polygone est égale à n fois l’aire d’un triangle.
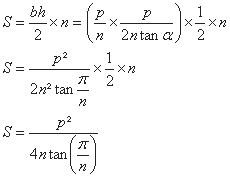
Soit g la fonction numérique définie sur I par ![]()
![]()

2.B On suppose que l’aire du polygone est constante et égale à S
On appelle Pn le périmètre du polygone régulier à n côtés dont l’aire est S.
Pn en fonction de S et n
On a vu plus haut que 
D’où


Pour une aire constante, le périmètre du polygone diminue quand le nombre de ses côtés augmente. Les abeilles auront donc tout intérêt à construire leurs ruches en utilisant des polygones dont le nombre de côtés sera le plus élevé possible, afin d'économiser de la cire.
Deuxième problème : Le fond des alvéoles - Aire de la surface latérale
On pose a=AB, I=AT et x=BK où x est un réel strictement positif. On note h(x) l'aire latérale de l'alvéole. h(x)=3(S1+S2+S3) où S1 est l'aire du trapèze AKUT, S2 l'aire du trapèze KCVU et S3 l'aire du losange ASCK. |
 |
Calcul des surfaces S1 et S2 :
Trapèze AKUT :
AB = hauteur = a
KU = petite base = I - x car BU = AT
AT = grande base = I
![]()
Or les trapèzes AKUT et KCUV sont identiques, d’où l’égalité
![]()
Et ![]()
APB est un triangle rectangle en B donc d'après le théorème de pythagore :

Aire S3 du losange ASCK :

Aire latérale de l'alvéole h(x) :

On pose 
Montrons que h(x) est minimum lorsque ![]() est minimum.
est minimum.


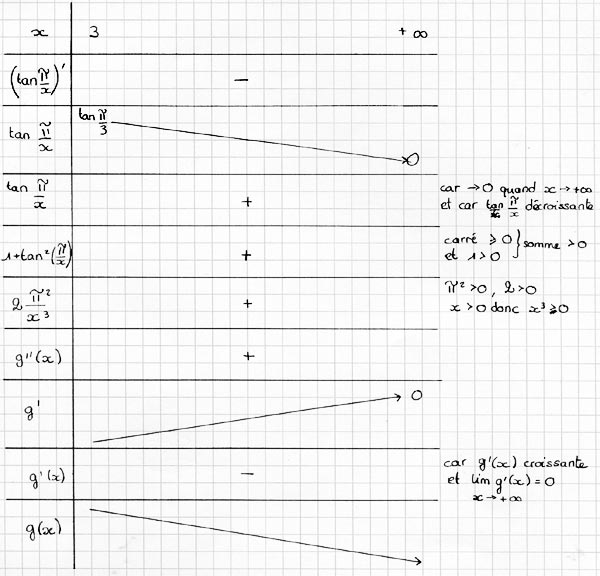
Etudions les variations de ![]()

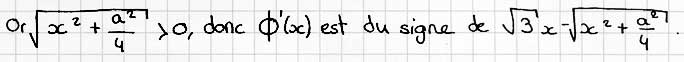


Tableau de variations de ![]() et h(x)
et h(x)

Et à présent, calculons la...


La connaissance de cet angle permet la construction aisée d'un patron d'alvéole.
Remarque : "Hé mais c'est pas le même résultat
que celui de Maraldi !"
En fait, 